İtalyan matematikçi Leonardo Fibonacci’nin (1170–1240) keşfettiği “Fibonacci dizisi”, kendinden önceki sayı ile toplanmasından oluşan bir sayı dizisidir. “Altın oran”, Fibonacci dizisindeki iki sayıdan büyük olanının küçük olana bölünmesi sonucu ortaya çıkan sayıdır.[1] Bu dizideki bir sayının kendinden bir önceki sayıya oranlanması sonucu altın oran (1,618) elde edilir.[2]
Altın oranın, ilk kimler tarafından keşfedildiği bilinmemektedir, fakat Mısırlıların ve Yunanlıların bu oran üzerine yaptığı birtakım çalışmalar olduğu görülmektedir. Öklid, milattan önce 300’lü yıllarda yazdığı Elementler adlı eserinde bir doğruyu 1,618 noktasından bölmekten bahsetmiş ve bunu “ekstrem ve önemli oranda” bölmek olarak adlandırmıştır.[3]
Birçok mimarî yapıda, birçok bitkide, Güneş Sistemimizde ve insan vücudunda altın orana rastlarız. Altın oran sayısı, matematikteki en gizemli sayı olarak kabul edilebilir. Leonardo da Vinci bu orana “İlahî oran” ismini vermiştir. Bu sayıya “saplantısı” olan Da Vinci, çeşitli araştırmalar yapmış ve dünyanın ilk altın oran ölçebilen pergelini icat etmiştir. Daha estetik ve güzel göründüğünden dolayı, hemen hemen bütün eserlerinde bu oranı kullanmaya özen göstermiştir.
Her şeyi nizam üzerine yaratan Rabbimiz, Furkan sûresinin ikinci âyetinde, “Her şeyi yaratıp nizam veren ve her şeyin varlığını bir ölçüye göre belirleyen O’dur.” buyurmuştur. Sadece bu âyette değil, Kur’ân-ı Kerim’in birçok yerinde, kâinattaki her şeyin belli bir ölçüde yaratıldığı vurgulanmıştır. Bilimsel araştırmalar sonucunda her şeyin belli bir oranda yaratıldığı ispatlanmıştır.
Gezegen yörüngelerinin eliptik yapısını keşfeden Johannes Kepler, Güneş Sisteminin yapısını altın oran kullanarak açıklamıştır. 1989 yılında Avustralya’daki Adelaide Üniversitesinde görev yapan Profesör Paul Davies tarafından yapılan araştırmada, dönen karadeliklerin termodinamiğinin altın oranla ilişkili olduğu görülmüştür.[4]
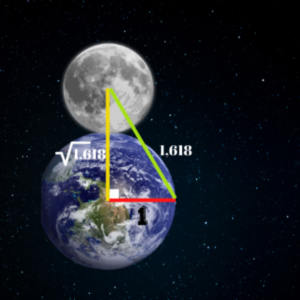
Rahman sûresinin beşinci âyetinde, Güneş ve Ay’ın belli bir hesaba bağlı olduğu vurgulanmıştır. Yapılan araştırmalara baktığımızda, Dünya ve Ay arasındaki mesafede de altın oranı görüyoruz. Dünya ve Ay’ın merkezleri bir hatla birleştirildiğinde oluşan dik üçgenin dik kenarı, altın oran sayısının karekökünü, üçgenin en uzun kenarı ise altın oranı vermektedir.[5]
Bitkilerde Altın Oran
Ayçiçeği sağa ve sola kıvrılan sarmal kollardan oluşur. Ancak soldaki spirallerin sayısı, sağdakilere eşit değildir. Soldaki ve sağdaki spiral kollar her zaman Fibonacci dizisinin ardışık iki sayısıdır.[6] Aynı şekilde, çam kozalağındaki taneler, soldan sağa ve sağdan sola sayıldığında çıkan sayı altın oran olacaktır.[7]
İnsanda Altın Oran
Araştırmacılar insan vücudunu incelemiş, anatomik özelliklerini tespit etmiş ve organların arasında da altın oran olduğu görülmüştür. Elimizde, baş parmağımız dışındaki parmaklarımızda bulunan boğumların ilk ikisinin toplamı, üçüncü boğumun ölçüsünü verir. Ayrıca insan yüzü de altın orana göre yaratılmıştır. Mesela üst çenedeki iki ön kesici dişin boylarına göre toplam genişliğinin altın oranı verdiğini görürüz.[8]
Akciğer ve kalb gibi organlarımızda da altın oran mevcuttur. 1985–1987 yılları arasında yapılan bir çalışmada, Dr. A.L Goldberger ve arkadaşları makalelerinde, akciğerin yapısında altın oranın varlığını tespit etmişlerdir. Soluk borusu, sağ ve sol olmak üzere iki ana bronşa ayrılır. Sağdaki kısa bronşun, soldaki uzun bronşa oranı her zaman 1/1,618’dir.[9]
Görüldüğü üzere, kâinattaki her şey bir ölçüye göre yaratılmaktadır. Altın oran; sonsuz ilme, kudrete ve iradeye işaret eden bir hakikattir. Eğer Allah’tan başka bir ilah olsaydı, bu mükemmel nizam olabilir miydi?
[1] tr.wikipedia.org/wiki/Altın_oran
[2] bilimgenc.tubitak.gov.tr/makale/fibonacci-dizisinden-altin-orana
[3] tr.wikipedia.org/wiki/Altın_oran
[4] www.theguardian.com/science/2003/jan/16/science.research1
[5] www.goldennumber.net/solar-system/
[6] asknature.org/strategy/fibonacci-sequence-optimizes-packing/
[7] awkwardbotany.com/2019/12/25/pine-cones-and-the-fibonacci-sequence/
[8] dergipark.org.tr/en/download/article-file/402091
[9] jcdr.net/articles/PDF/13317/42772_PD_(V-2-PK_PrG_OM_SL)_GC(PrG_KM_OM)_PN(SL).pdf




